Exemplary Info About How To Find M And By Mx B
Understanding the Mighty mx + b
1. What's the Deal with mx + b?
Ever looked at an equation that looks like a jumble of letters and felt a slight panic? Don't worry, you're not alone! But the good news is, equations like y = mx + b are actually pretty straightforward once you get the hang of them. It's a powerful little formula that describes a straight line, and understanding it unlocks a whole world of graph-reading and problem-solving abilities.
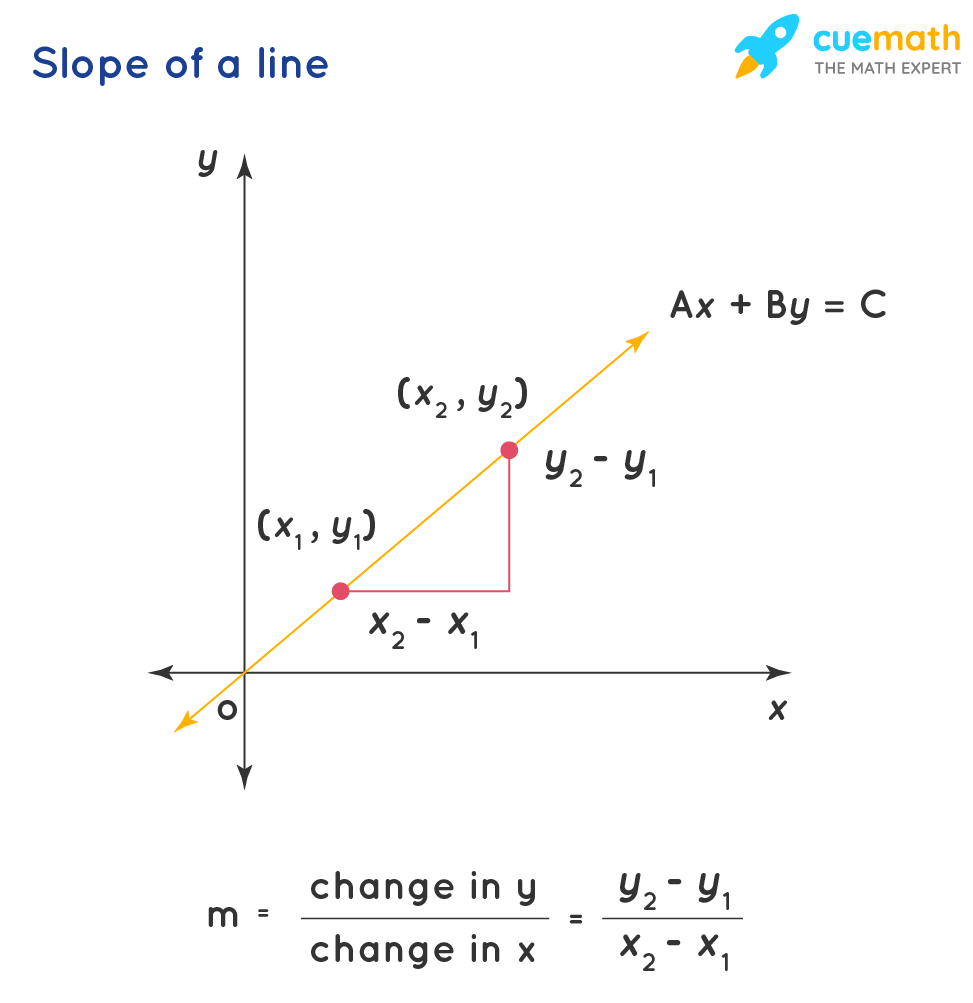
Think of y = mx + b as the secret decoder ring for straight lines. Each letter plays a specific role. 'y' and 'x' are the coordinates of any point on the line (like plotting a course on a map). The 'm' and 'b'? Those are our key players today. They define the line's character. 'm' tells us how steep the line is (its slope), and 'b' tells us where the line crosses the vertical axis (the y-intercept). So, 'm' and 'b' are basically the line's personality, determining its direction and starting point. We want to find them.
This isn't just some abstract math concept, either. Understanding y = mx + b has real-world applications! Imagine you're tracking the growth of a plant over time. The 'm' could represent how much the plant grows each day, and the 'b' could be its initial height. Or maybe you're calculating the cost of a taxi ride. 'm' could be the price per mile, and 'b' the initial fare you pay just for getting in. See? It's practical!
So, let's dive in and demystify this equation. We'll break down exactly how to find 'm' and 'b', so you can confidently tackle any problem involving straight lines. Prepare to become a linear equation ninja!
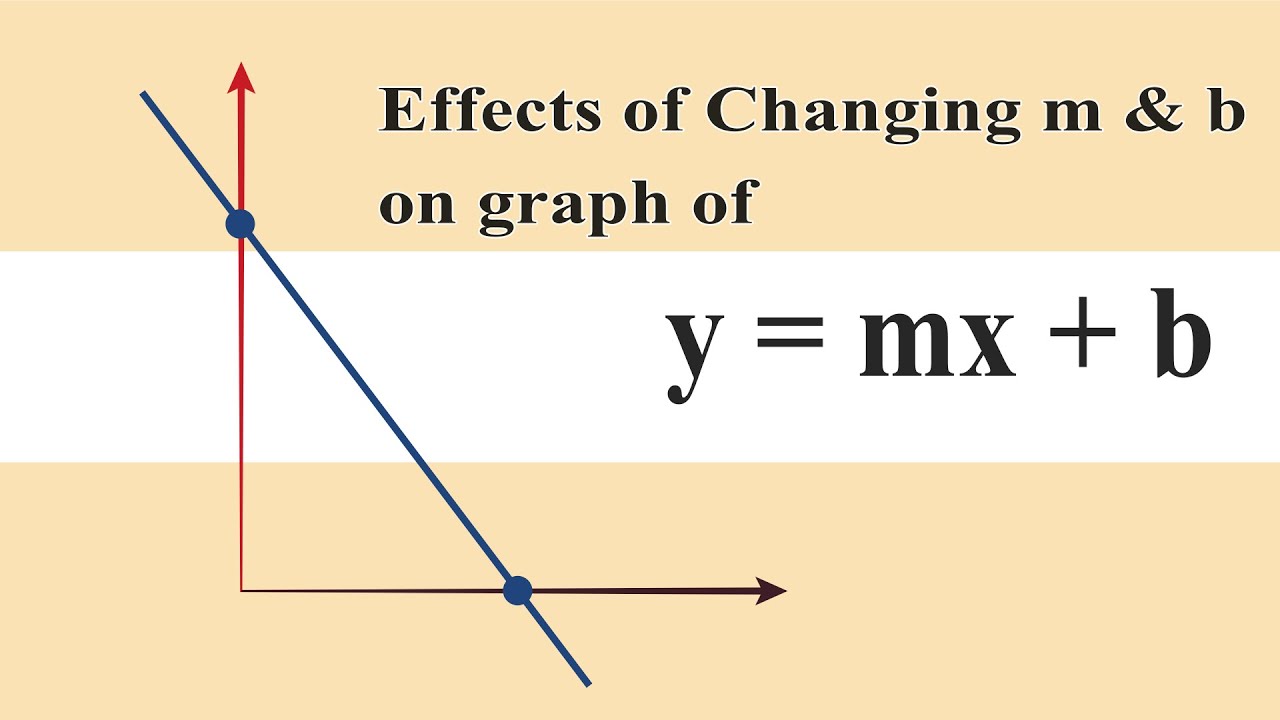
Cracking the Code
2. The Rise Over Run Method
Alright, let's get down to business and figure out how to find 'm', the slope. The slope is all about how steep the line is. Is it a gentle incline, a sheer cliff, or perfectly flat? The slope tells us! Think of it like this: If you were walking along the line from left to right, would you be going uphill (positive slope), downhill (negative slope), or staying on level ground (zero slope)?
The classic way to calculate slope is using the "rise over run" method. Imagine you have two points on the line. The 'rise' is the vertical change between the two points (how much you go up or down), and the 'run' is the horizontal change between the two points (how much you go left or right). Divide the rise by the run, and you've got your slope!
Mathematically, it looks like this: m = (y2 - y1) / (x2 - x1). Don't let the subscripts scare you! It just means you're subtracting the y-coordinate of the first point from the y-coordinate of the second point, and then dividing by the difference between the x-coordinates of those same points. Just be consistent with which point you label as "point 1" and "point 2."
Let's say you have two points: (1, 3) and (4, 9). The rise is 9 - 3 = 6, and the run is 4 - 1 = 3. So, the slope is 6 / 3 = 2. This means that for every 1 unit you move to the right along the line, you move up 2 units. Pretty neat, huh?
Y Mx+b How To Graph
Locating 'b'
3. Where the Line Meets the Y-Axis
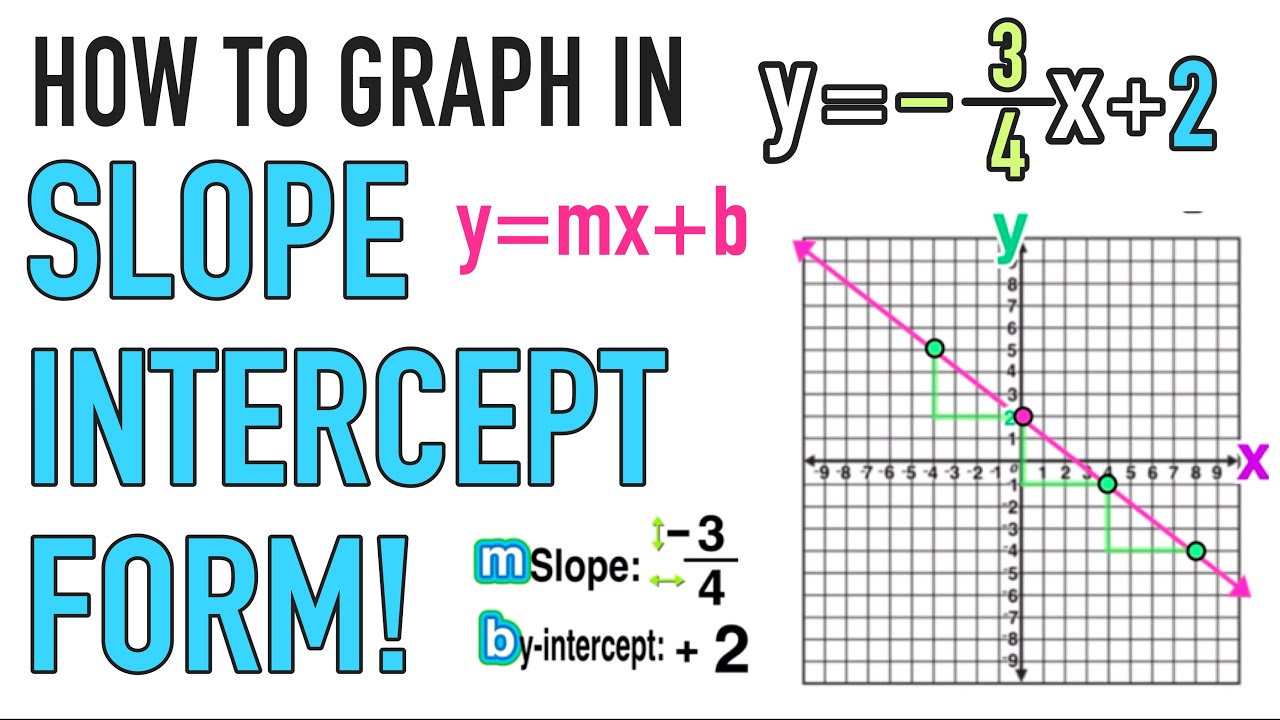
Now, let's track down 'b', the y-intercept. The y-intercept is simply the point where the line crosses the y-axis (the vertical axis). It's the 'starting point' of the line, so to speak. Visually, it's easy to spot on a graph — just look where the line intersects the y-axis. The y-coordinate of that intersection is your 'b' value.
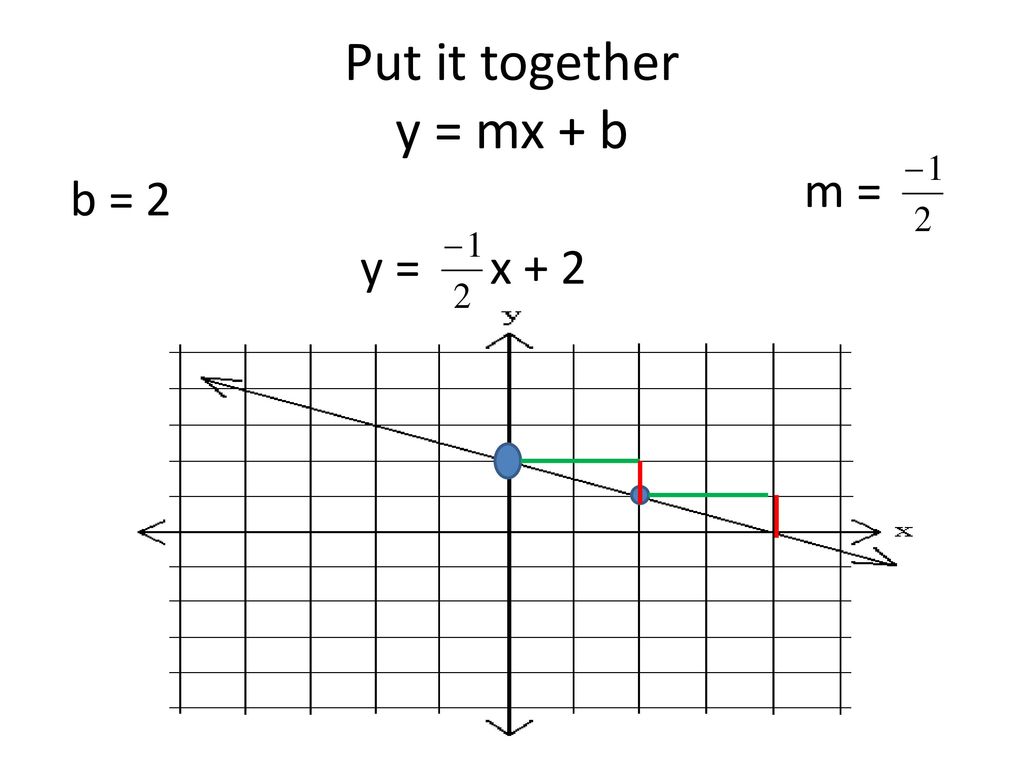
If you're given the equation of the line (y = mx + b) and you already know the slope 'm', finding 'b' is relatively simple. Just pick any point (x, y) that lies on the line (it can be any point!), plug its coordinates and the value of 'm' into the equation, and solve for 'b'. For example, lets say we know m=2 and the line passes through the point (3,7). Plug those values into y=mx+b and we get 7=2 3+b. Therefore, b=1!
Sometimes you might have the slope (m) and one point (x,y) on the line. You can still find 'b'!. The equation y=mx+b is your friend. Just plug the x, y, and m values in and solve for b.
So, finding 'b' is all about knowing where the line crosses that important vertical line. The y-axis is the point from which everything else is relative in the graph.
Putting it All Together: Finding m and b with Two Points
4. The Ultimate Equation-Solving Strategy
Let's ramp up the challenge a bit! What if you're only given two points on the line and asked to find both 'm' and 'b'? No sweat! You've got all the tools you need.
First, use those two points to calculate the slope 'm' using the "rise over run" formula we discussed earlier: m = (y2 - y1) / (x2 - x1). Once you've got 'm', you're halfway there! This is where it gets interesting. We have "m", x and y. We need to find "b", so plug into the equation. y=mx+b, then b=y-mx
Select one of the two points. It doesn't matter which one you choose; you'll get the same value for 'b' either way. Plug the x and y coordinates of your chosen point, along with the 'm' value you just calculated, into the equation y = mx + b. Now, solve the equation for 'b'. Voila! You've found both 'm' and 'b', and you've completely defined the straight line!
For instance, say we have points (2,5) and (4,9) to find "m" first. By m = (y2 - y1) / (x2 - x1) — m=(9-5)/(4-2) , so m=2. Plugging the point (2,5) to get "b", we know y = mx + b. Then 5=2(2)+b so b=1. Now we have m and b. It's easy right?
Real-World Examples: When mx + b Comes to the Rescue
5. From Budgeting to Ballistics: The Power of Linear Equations
Okay, so we've mastered the math. But where does all this 'm' and 'b' stuff actually matter in the real world? Turns out, linear equations pop up in all sorts of unexpected places!
Think about budgeting. Let's say you start with $100 and save $20 each week. Your total savings (y) can be represented by the equation y = 20x + 100, where 'x' is the number of weeks. The slope ('m' = 20) tells you how much your savings increase each week, and the y-intercept ('b' = 100) represents your initial savings. You can use this equation to predict how much money you'll have after a certain number of weeks or how long it will take to reach a specific savings goal. Amazing!
Another example is calculating the distance a car travels at a constant speed. If a car travels at 60 miles per hour (mph), the distance (y) it covers in 'x' hours can be represented by the equation y = 60x. Here, the slope ('m' = 60) is the speed of the car, and the y-intercept ('b' = 0) is the initial distance (assuming the car starts at a distance of zero). Want to know how far the car travels after 3 hours? Just plug in x = 3 and solve for y: y = 60 3 = 180 miles.
From physics to finance, understanding y = mx + b can help you make sense of the world around you and solve practical problems. So, the next time you see a straight line, remember that there's a powerful equation behind it, waiting to be unlocked!
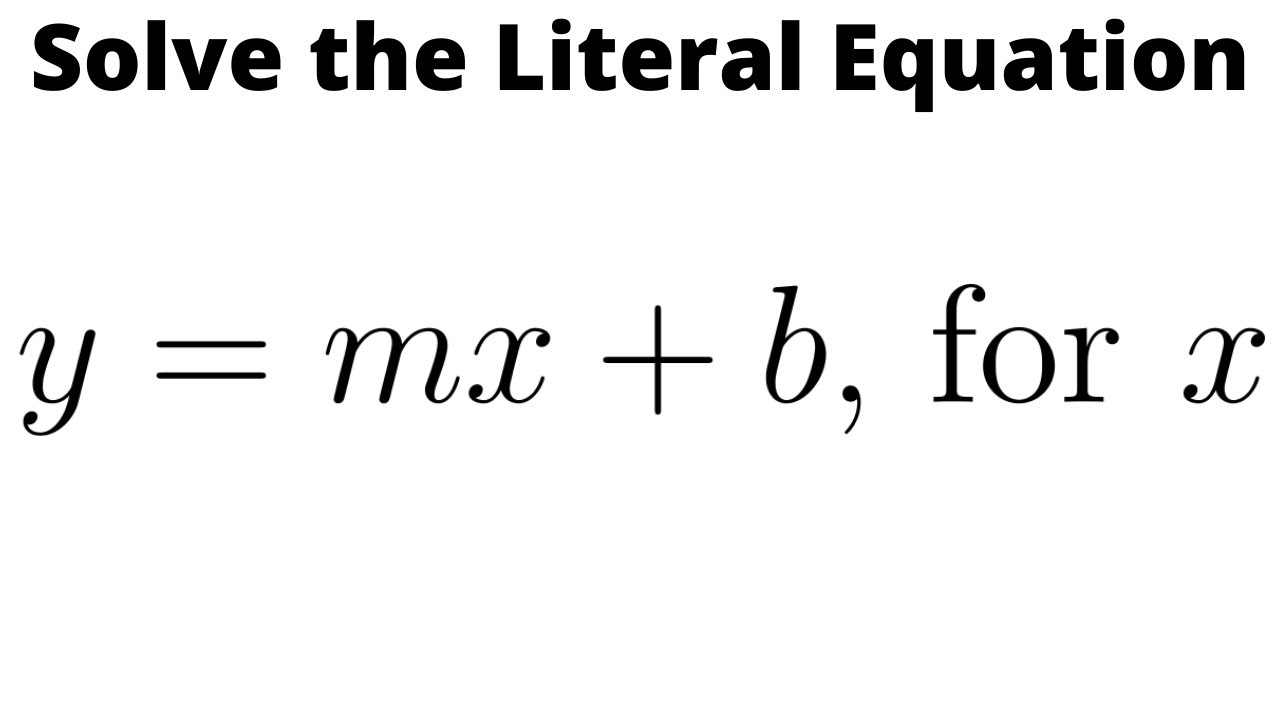
Frequently Asked Questions (FAQs)
6. Answering Your Burning Questions About m and b
Q: What happens if the slope ('m') is zero?A: If 'm' is zero, the line is horizontal. In that case, the equation becomes y = b. This means that the y-value is constant, regardless of the x-value. It's a flat line that doesn't go up or down.
Q: Can the slope ('m') be undefined? What does that look like?A: Yes! The slope is undefined when the line is vertical. This happens when the 'run' (the change in x) is zero. You can't divide by zero, so the slope is undefined. A vertical line has the equation x = a, where 'a' is the x-intercept (the point where the line crosses the x-axis).
Q: Is it possible for 'b' to be zero? What does that mean?A: Absolutely! If 'b' is zero, the line passes through the origin (the point where the x-axis and y-axis intersect, also known as (0,0)). In this case, the equation becomes y = mx. The line starts at the center point of the graph!
Q: How does a negative slope ("m") look on a graph?A: A negative slope means that as you move from left to right along the line, you're going downhill. It slopes downward. The steeper the negative slope, the faster you're descending.
Q: Can I use any two points on a line to find the slope?A: Yes! As long as the two points are distinct and lie on the same straight line, you can use them to accurately calculate the slope. The slope is constant throughout the entire line, so it doesn't matter which two points you choose.
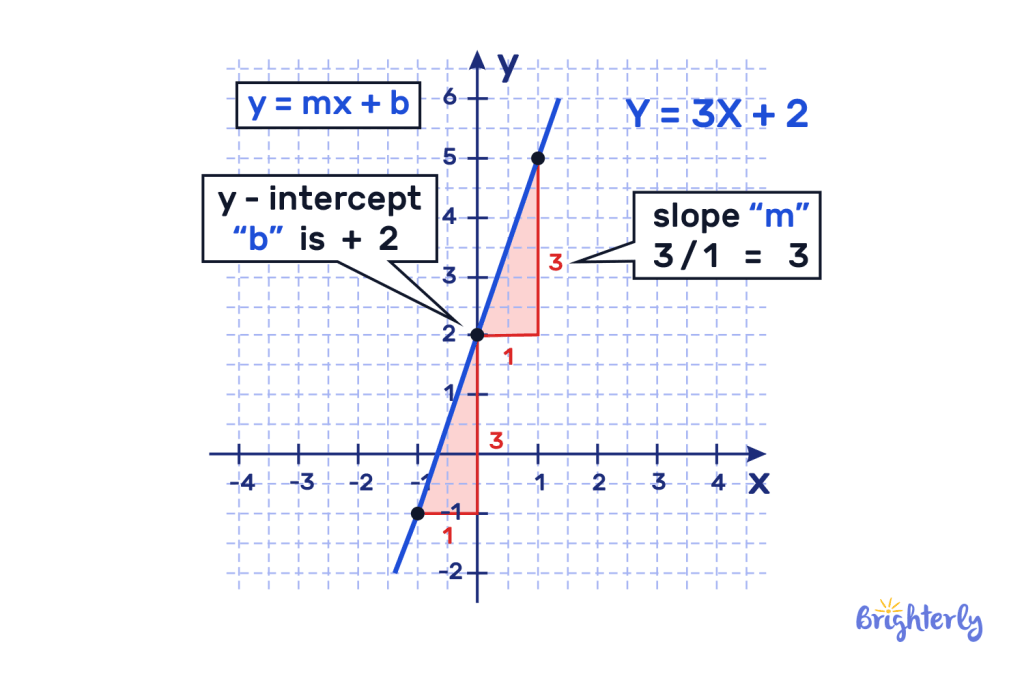
Y = Mx + B Definition, Slope Intercept Form, Examples, Facts