Who Else Wants Info About Is A 2 Bit Adder Full

Unraveling the Adder Enigma

So, you're diving into the fascinating world of digital logic and adders, eh? Excellent choice! It's like understanding the plumbing of your computer, only instead of water, we're dealing with bits. You might be wondering, "Is a 2-bit adder just a fancy name for a full adder?" Well, the answer, as with many things in engineering, is a bit more nuanced than a simple "yes" or "no." Let's break it down, shall we?

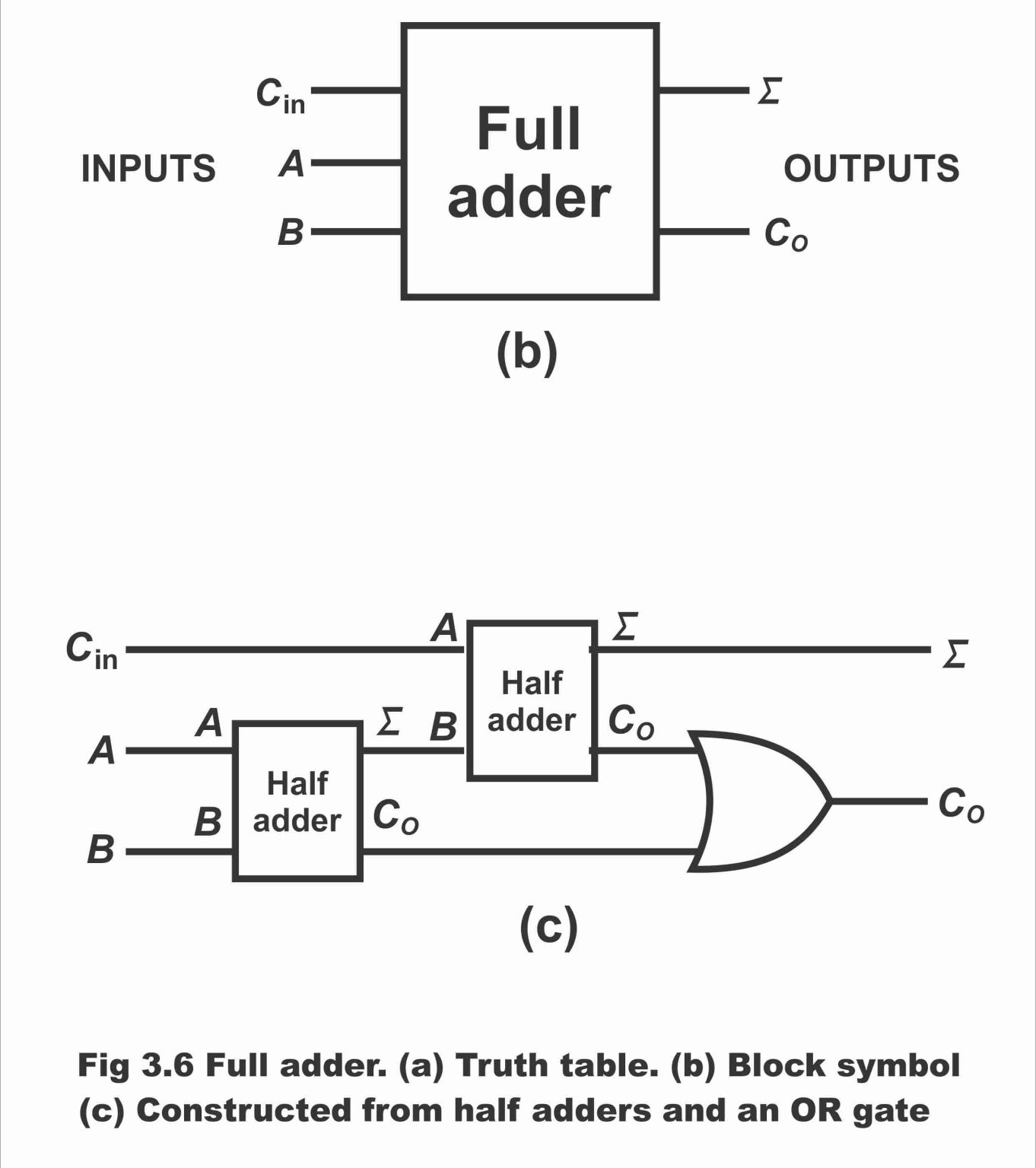
Think of a full adder like a single Lego brick. It's a fundamental building block. A full adder takes three inputs: two bits to be added (let's call them A and B) and a carry-in bit (Cin) from a previous stage. It then produces two outputs: a sum bit (S) and a carry-out bit (Cout) that will be used as the carry-in for the next stage. It's the workhorse of addition!

Now, imagine building something bigger, like a Lego castle. You wouldn't use just one brick, would you? You'd need many, connected together. A 2-bit adder is similar. It's designed to add two 2-bit numbers. But it achieves this feat by using, you guessed it, full adders (and sometimes a half adder too!).

Therefore, while a full adder is a crucial component within a 2-bit adder, the 2-bit adder itself is a complete circuit designed for a specific purpose: adding two 2-bit numbers. It's like saying a car's engine is the whole car. It's vital, but it's not the entire picture.

1. The Inner Workings

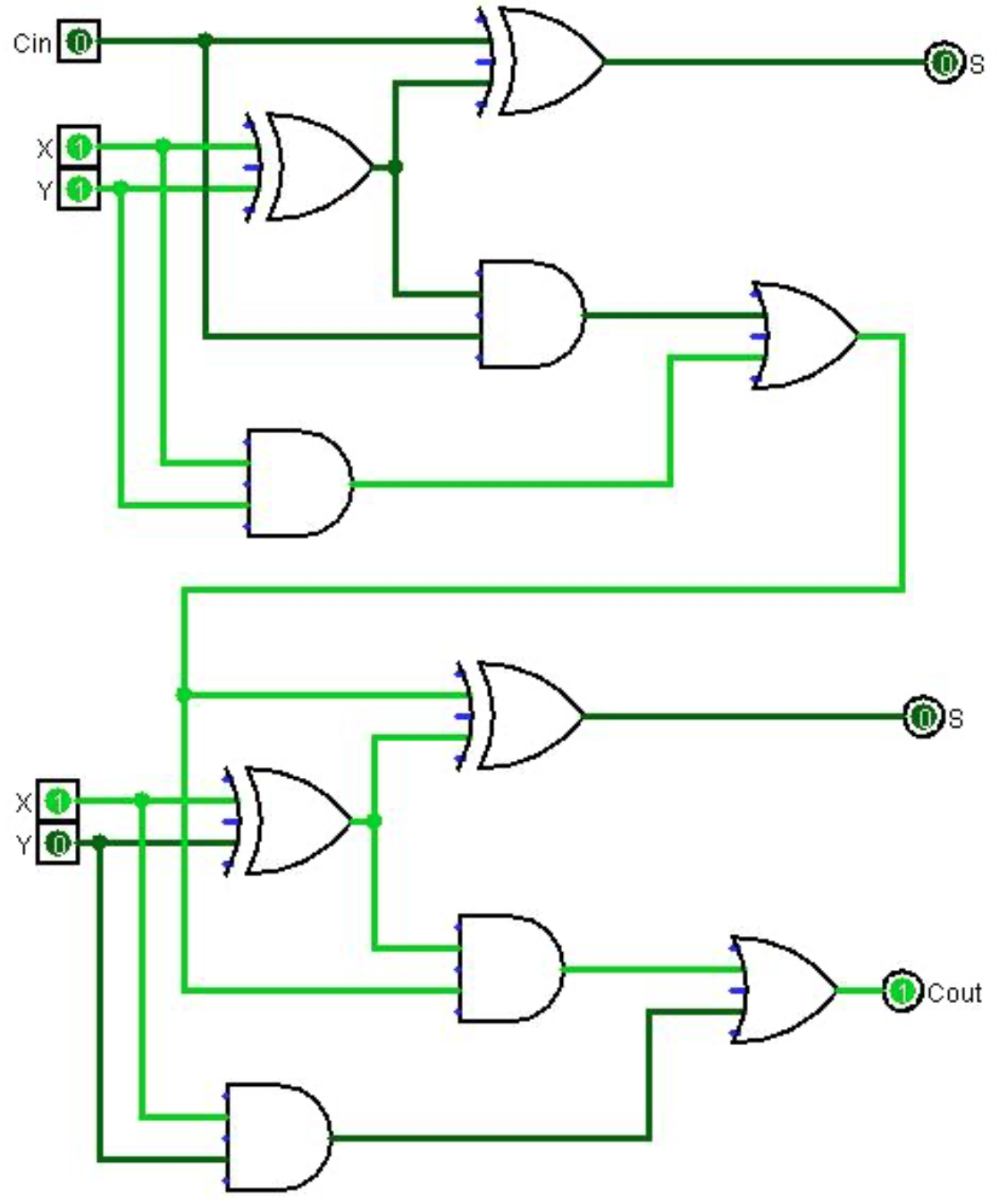
Let's peek under the hood of a typical 2-bit adder. You'll usually find it built using a combination of full adders. Often, it will be composed of two full adders chained together. But why two? Well, the first full adder handles the least significant bits (LSBs) of the two numbers you're adding. The second full adder tackles the most significant bits (MSBs), taking the carry-out from the first adder as its carry-in.

Consider adding the numbers 10 (2 in decimal) and 01 (1 in decimal). The first full adder would add the rightmost bits (0 and 1), with an initial carry-in of 0. The second full adder would add the leftmost bits (1 and 0), using the carry-out from the first adder as its carry-in. This chaining effect allows the 2-bit adder to correctly perform binary addition across both bits.

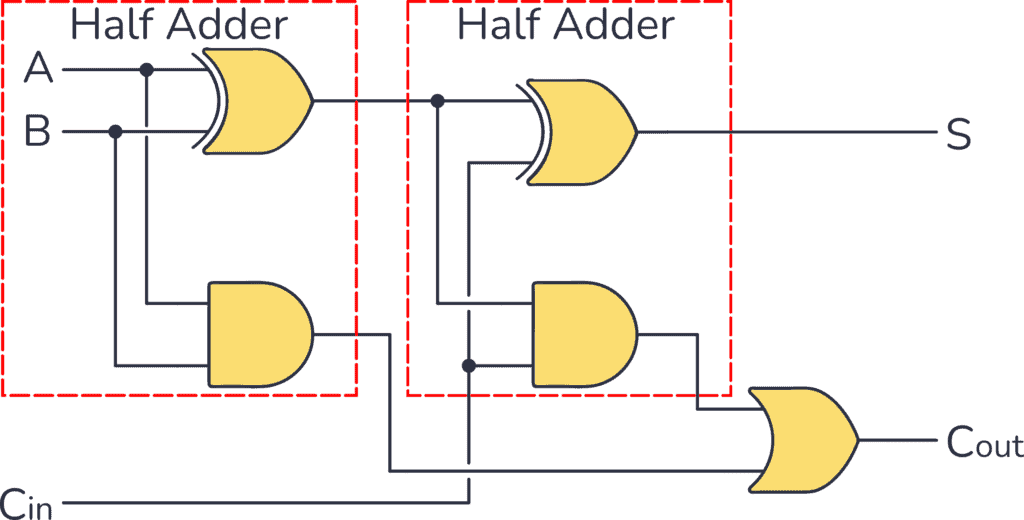
You might also encounter 2-bit adders using a half-adder for the first stage and a full adder for the second stage. The half-adder only deals with two inputs (A and B) and produces a sum and carry-out. Since the least significant bit doesn't need a carry-in, a half-adder can be more efficient. Then, the full adder handles the MSBs with the carry-out from the half-adder.

Think of it like this: building a 2-bit adder from full adders is like using pre-fabricated walls to build a room. You could build the walls from individual bricks, but why would you when you can use a larger, more convenient component? The full adder is that "pre-fabricated wall" for binary addition.

Beyond the Basics

2. Exploring the Ripple Effect

The most straightforward way to build a multi-bit adder (like our 2-bit example) is to chain full adders together, where the carry-out of one stage becomes the carry-in of the next. This is known as a ripple carry adder. The "ripple" refers to the way the carry signal propagates through the adder, like a ripple in a pond.

While simple to understand and implement, ripple carry adders have a significant drawback: speed. The carry signal has to propagate through each stage sequentially. For larger adders (think 32-bit or 64-bit), this delay can become substantial, limiting the overall performance of the system. Imagine waiting for a message to be passed through a long line of people; the longer the line, the longer the wait!

Despite the speed limitations, ripple carry adders are still used in some applications where simplicity and low cost are more important than speed. They're often used in educational settings to illustrate the fundamental principles of binary addition.

It's worth noting that optimizing a ripple carry adder is difficult, as the carry signal must propagate sequentially. There are alternative architectures designed to improve speed performance, such as carry-lookahead adders.

3. Faster Alternatives

To overcome the speed limitations of ripple carry adders, engineers have developed more advanced adder architectures. One such architecture is the carry-lookahead adder. This design uses logic gates to predict the carry-out signals for each stage, rather than waiting for them to ripple through. This significantly reduces the propagation delay and improves the overall speed of the adder.

Another approach involves using carry-select adders. These adders pre-compute the sum and carry for both possible carry-in values (0 and 1) and then select the correct result based on the actual carry-in signal. This allows for faster addition because the calculations are done in parallel.

These more complex adder designs involve a trade-off between speed and complexity. Carry-lookahead and carry-select adders require more logic gates than ripple carry adders, which means they are more expensive to implement. However, the speed benefits are often worth the cost, especially in high-performance applications.

The best type of adder depends on the specific requirements of the application. For simple, low-cost applications, a ripple carry adder may be sufficient. For high-performance applications, a carry-lookahead or carry-select adder may be necessary.

Full Adder vs. Half Adder

4. Differentiating the Adders

Just to solidify things, let's recap the key differences between full adders and half adders. The most crucial distinction is the number of inputs. A half adder takes two inputs (A and B), while a full adder takes three (A, B, and Cin).

This extra input allows the full adder to handle carry-in signals from previous stages, making it suitable for multi-bit addition. A half adder, on the other hand, is primarily used for adding the least significant bits where no carry-in is initially present.

In terms of outputs, both half adders and full adders produce a sum (S) and a carry-out (Cout). However, the logic equations for calculating these outputs are different for each type of adder due to the presence of the carry-in input in the full adder.

Therefore, while both types of adders are essential building blocks in digital circuits, they serve distinct purposes. Half adders are like the "starter" adders, while full adders are the "all-rounders" capable of handling more complex addition scenarios.

Practical Applications

5. Adders in Action

So, where do these adders actually get used? Everywhere! Seriously. Any digital system that performs arithmetic operations relies on adders in some form. Consider your computer's central processing unit (CPU). Adders are fundamental to its arithmetic logic unit (ALU), which performs all the calculations that keep your computer running.

Beyond computers, adders are also found in digital signal processors (DSPs), which are used in audio and video processing, communication systems, and control systems. In these applications, adders are used to perform operations like filtering, modulation, and demodulation.

Even simple devices like calculators rely on adders to perform basic arithmetic functions. From pocket calculators to supercomputers, adders are the unsung heroes of digital computation.

Think about image processing. Adding pixel values is a key component in many image editing and enhancement techniques. Or consider cryptography. Adders play a role in encryption and decryption algorithms, securing your online transactions and communications.

The Verdict

So, to definitively answer the original question: No, a 2-bit adder isn't just a full adder. It uses full adders (or a combination of half and full adders) as building blocks to perform the specific task of adding two 2-bit binary numbers. It's a complete circuit designed for a specific function, while a full adder is a more general-purpose component.

It's all about context. A full adder is a tool, and a 2-bit adder is a tool box built using those tools for a specialized job. Understanding the difference is key to grasping the fundamentals of digital logic design.

Hopefully, this has shed some light on the relationship between full adders and 2-bit adders. Now you can impress your friends with your knowledge of binary arithmetic (or, at least, not be completely lost when the topic comes up at your next cocktail party!).

Keep exploring! The world of digital logic is vast and fascinating. And who knows, maybe you'll be the one designing the next generation of high-speed adders.

Frequently Asked Questions (FAQs)

6. Your Burning Adder Questions Answered

Still have some lingering questions about adders? Fear not! Here are a few frequently asked questions to further clarify the concepts:

Q: Can I build a 3-bit adder using only full adders?

A: Absolutely! You would need three full adders, chaining the carry-out of each stage to the carry-in of the next. The first full adder would have a carry-in of 0 (or you could use a half adder for the first stage).

Q: Why are carry-lookahead adders faster than ripple carry adders?

A: Carry-lookahead adders use logic gates to predict the carry-out signals, instead of waiting for them to propagate through each stage sequentially like in a ripple carry adder. This parallel calculation significantly reduces the overall delay.

Q: Are there any other types of adders besides ripple carry and carry-lookahead?

A: Yes! Other types of adders include carry-select adders, conditional sum adders, and even more complex architectures designed for specific performance requirements.