Exemplary Info About What Is Euler's Path

Navigating Networks

1. A Stroll Through Mathematical History

Ever heard of a mathematical walk where you trace every street in town exactly once? Well, that's the essence of an Euler's path. The concept itself is named after the brilliant Swiss mathematician Leonhard Euler, who, back in the 18th century, tackled a puzzling problem in the city of Knigsberg (now Kaliningrad, Russia). This puzzle involved figuring out if it was possible to cross all seven bridges of the city without crossing any bridge more than once. Euler not only solved the puzzle but, in doing so, laid the foundation for what we now know as graph theory and the elegant concept of Euler's paths.

Imagine you're planning a walking tour of your neighborhood. You want to see every street, but you're also trying to conserve energy (and shoe leather!). An Euler's path provides the perfect route, ensuring you cover every street exactly once, and saving you from unnecessary backtracking. It's a practical problem with a surprisingly theoretical solution!

Now, you might be thinking, "Is this just some abstract math thing with no real-world application?" Far from it! Euler's paths pop up in surprising places, from designing efficient delivery routes to optimizing computer networks. Think about it: a delivery company wants to minimize the distance its trucks travel, or a network engineer wants to ensure data packets travel the most efficient path. Understanding Euler's paths helps them accomplish those goals.

So, what exactly makes an Euler's path possible? It all boils down to the connections, or "vertices" and "edges," in a graph. A graph, in this context, is just a collection of points (vertices) connected by lines (edges). Euler figured out a clever trick involving the "degree" of each vertex — the number of edges connected to it. Stay tuned, and we'll unravel this trick together!

The Secret Sauce

2. Decoding Euler's Rules

Alright, let's get into the nitty-gritty (okay, maybe just the slightly-more-detailed) part of what makes an Euler's path tick. The key is understanding the "degree" of each vertex in your graph. As we said before, the degree of a vertex is simply the number of edges connected to it. So, if a vertex has three lines coming out of it, its degree is three.

Euler discovered that for a graph to have an Euler's path, it can have at most two vertices with an odd degree. All the other vertices must have an even degree. Why is this? Well, think about it like this: if you enter a vertex on one edge, you need to be able to leave it on another edge. That requires an even number of connections. The two odd-degree vertices, if they exist, represent the starting and ending points of your path. You start on one, traverse the entire graph, and end on the other.

But wait, there's more! Not only do you need the right degrees, but your graph also needs to be "connected." This means you can get from any vertex to any other vertex by following the edges. If your graph is in two separate, non-connected pieces, you're not going to be able to trace the whole thing in a single path. It's like trying to walk through two completely different cities at the same time — physically impossible!

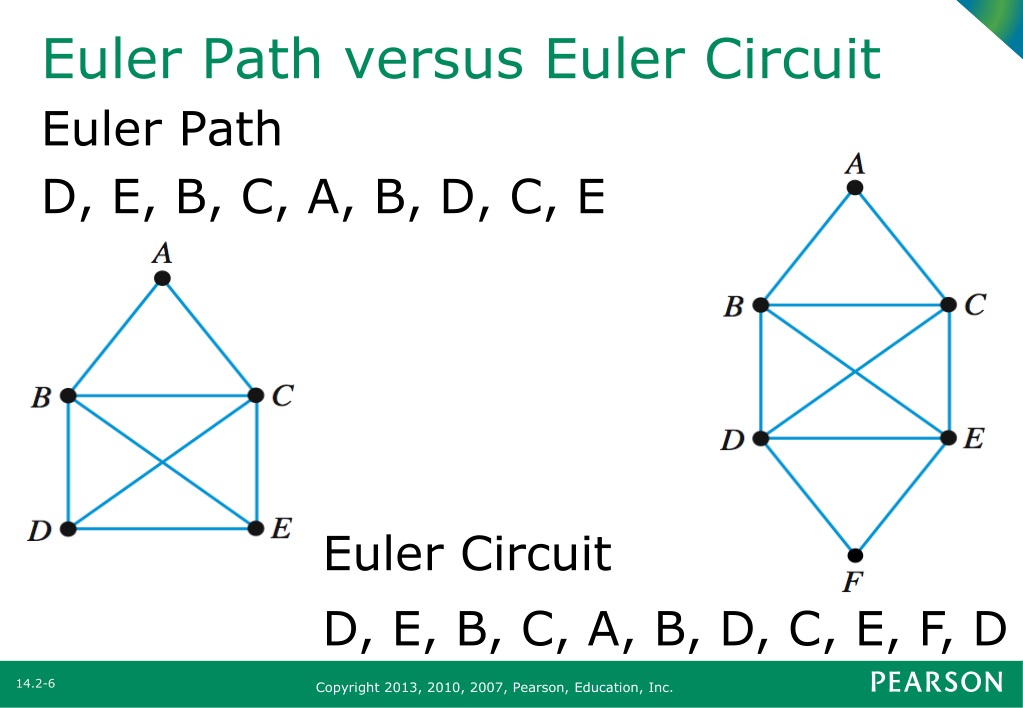
Imagine a simple graph with four vertices, A, B, C, and D. A is connected to B and C, B is connected to A and D, C is connected to A and D, and D is connected to B and C. Each vertex has a degree of 2 (even). This graph has an Euler circuit, meaning you can start at any vertex and end up back at the same vertex after traversing every edge exactly once. Fun, right?

Euler's Path vs. Euler's Circuit

3. Closing the Loop

Now that we've explored Euler's paths, let's introduce its cousin: the Euler circuit. Both involve traversing every edge exactly once, but there's a key difference: an Euler circuit starts and ends at the same vertex. It's a closed loop, a mathematical circle if you will. Think of it as taking a scenic tour and ending up right back where you started — super convenient!

So, what does it take for a graph to have an Euler circuit? The rule is even stricter than for an Euler's path. For a graph to have an Euler circuit, every vertex must have an even degree. No exceptions! Why? Because if you start at a vertex and end at the same vertex, you need to have an equal number of "ins" and "outs" for each point along the way.

Think of a perfectly symmetrical shape, like a square or a hexagon, where each corner (vertex) connects to exactly two sides (edges). These shapes readily lend themselves to Euler circuits. You can start at any corner, trace the entire perimeter, and end up right back where you began.

To cement the difference, consider these scenarios: a graph with vertices A, B, and C where A connects to B, B connects to C, and C connects to A has an Euler circuit. However, if we add a fourth vertex, D, and connect it only to A, the graph only has an Euler's path (starting at D and ending at either B or C) but no Euler circuit because vertices A and D now have odd degrees.

Real-World Applications

4. From Deliveries to DNA

Okay, so we've established that Euler's paths and circuits are interesting mathematical concepts. But where do they actually show up in the real world? Turns out, they're surprisingly useful in a variety of fields!

One of the most obvious applications is in route optimization. Imagine a delivery truck driver who needs to visit several locations and wants to minimize the total distance traveled. By representing the locations as vertices and the roads as edges, they can use algorithms based on Euler's paths to find the most efficient route, saving time, fuel, and money. The same principle applies to street sweeping, garbage collection, and even postal delivery.

Another fascinating application is in DNA sequencing. Scientists use fragments of DNA to reconstruct the entire sequence of a gene. This process can be modeled as finding an Euler's path in a graph where the fragments are represented as vertices and the overlaps between them are represented as edges. By finding the right path, they can piece together the complete genetic code.

Beyond that, Euler's paths are also used in network design, circuit board testing, and even creating mazes! Whenever you need to traverse a set of connections in an efficient and organized way, Euler's paths provide a powerful tool.

Finding an Euler's Path

5. Solving the Puzzle

So, you're faced with a graph, and you want to know if it has an Euler's path and, if so, how to find it. Here's a simplified step-by-step guide:

First, check for connectivity. Make sure that you can reach every vertex from every other vertex by following the edges. If the graph is disconnected, you can't find an Euler's path.

Next, count the degrees of each vertex. If there are more than two vertices with an odd degree, then no Euler's path exists. If there are exactly two vertices with an odd degree, those vertices will be the start and end points of your Euler's path. If all vertices have even degrees, you have an Euler circuit, and you can start at any vertex.

Finally, start tracing your path. There are algorithms (like Fleury's algorithm) that can help you systematically traverse the graph, ensuring you visit every edge exactly once. The basic idea is to choose an edge to travel along, mark it as visited, and continue to the next vertex. Be careful not to choose an edge that disconnects the remaining unvisited part of the graph unless you have no other choice!

Finding Euler's Path isn't always easy, but there are many tools and program that can help. With the correct implement, you can use Euler's Path in many different area of expertise.

FAQ About Euler's Path

6. Your Questions Answered

Here are some frequently asked questions about Euler's paths to further clarify the concept:

Q: Can a graph have multiple Euler's paths?

A: Absolutely! If a graph has an Euler's path, there can be multiple valid paths, especially if there are multiple choices of edges to traverse at each vertex. The specific path you find will depend on the order in which you choose the edges.

Q: What happens if a graph has zero vertices with odd degrees?

A: If a graph has no vertices with odd degrees (i.e., all vertices have even degrees) then the graph has an Euler circuit. This means you can start at any vertex and traverse the entire graph, returning to your starting point. It's a special case of Euler's path where the start and end are the same.

Q: Is there a quick way to determine if a very large graph has an Euler's Path without checking every single vertex and edge?

A: While you still need to check the degree of each vertex to be absolutely sure, focusing on connectivity first can save time. If a large graph is obviously disconnected, you don't need to check degrees at all, as it cannot have an Euler's Path. Also, you can use algorithms to check the connectivity and degree in parallel, reducing overall processing time.