Peerless Tips About What Does Ax2 Bx C Mean

Factor Quadratic Trinomials Calculator
Unlocking the Secrets of ax2 + bx + c: A Gentle Guide
1. Deciphering the Quadratic Code
Ever stared blankly at the equation ax2 + bx + c and felt like you were looking at ancient hieroglyphics? You're not alone! This little expression is actually a cornerstone of algebra, a friendly face (once you get to know it) hiding in plain sight. Think of it as a mathematical puzzle with a satisfying solution just waiting to be discovered.
At its core, ax2 + bx + c represents a quadratic expression. "Quadratic" simply means it involves a variable raised to the power of two (that's the "2" part). The 'a', 'b', and 'c' are just coefficients—numbers that sit in front of the variable 'x' (and the constant term). These coefficients are important because they influence the shape and position of the graph that represents this equation, a parabola. So, basically, they're the key players in this mathematical drama.
Why should you care about this seemingly abstract formula? Well, quadratic equations pop up everywhere in the real world! From calculating the trajectory of a ball thrown in the air (thanks, gravity!) to designing the curves of bridges and arches, they're essential tools for engineers, physicists, and even game developers. Learning to understand them is like unlocking a superpower in problem-solving.
So, lets break it down further, shall we? Think of 'x' as the unknown we're trying to solve for, the missing piece of the puzzle. The coefficients 'a', 'b', and 'c' are the clues we use to find that missing piece. The whole equation is about finding the values of 'x' that make the equation true, often meaning it equals zero. It's like a mathematical treasure hunt where 'x' marks the spot!

The A, B, C's of Coefficients
2. Understanding the Roles They Play
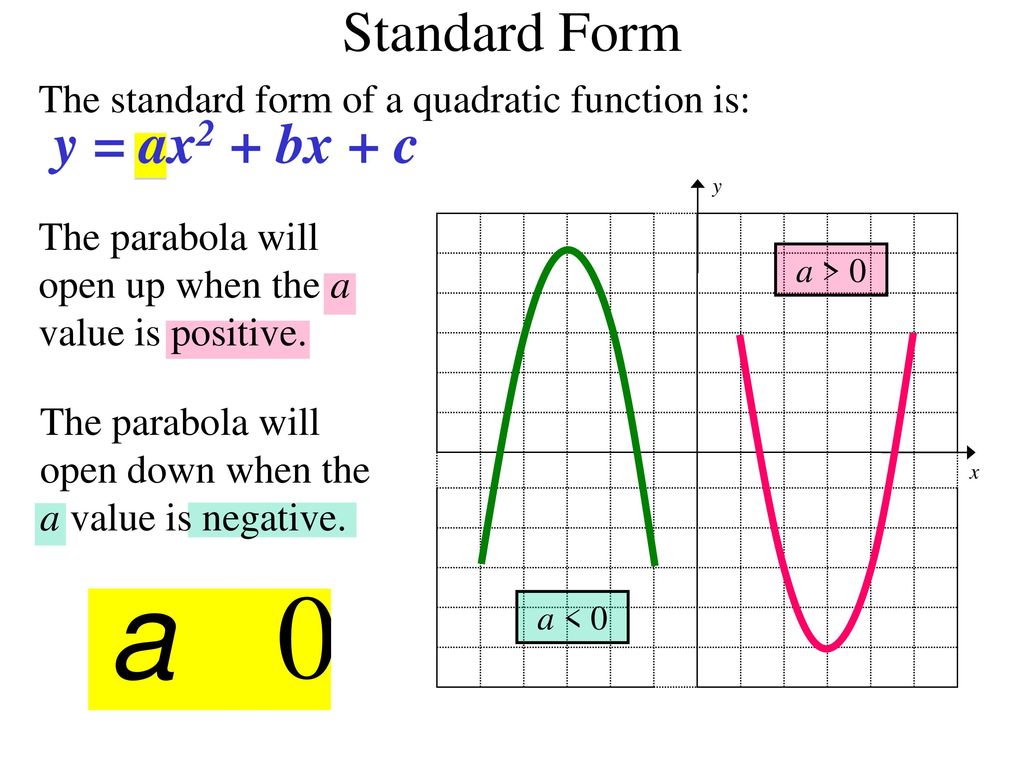
Let's take a closer look at those coefficients, a, b, and c. Each one has a specific job to do in shaping the quadratic equation and its corresponding parabola. Think of 'a' as the director of the parabola's opening direction. If 'a' is positive, the parabola opens upwards, like a happy face (U). If 'a' is negative, it opens downwards, like a sad face (_) . 'a' also controls how "wide" or "narrow" the parabola is. A large value of 'a' makes the parabola narrower, while a smaller value makes it wider.
The coefficient 'b' is a bit trickier. It affects the position of the parabola's vertex (the turning point) and its axis of symmetry. It works in tandem with 'a' to determine how far left or right the parabola shifts from the y-axis. The relationship between 'a' and 'b' dictates the horizontal placement of the vertex. In simpler terms, 'b' kind of nudges the parabola around the graph.
Finally, we have 'c', the constant term. This one's the easiest to understand. 'c' represents the y-intercept of the parabola, which is the point where the parabola crosses the y-axis. So, if you know the value of 'c', you immediately know one point on the parabola. It's like a freebie point to help you sketch the graph! If you graph the equation on a typical Cartesian plane, 'c' will be where the line intersects the y-axis.
Together, a, b, and c create a symphony of influences that determine the appearance and behavior of the quadratic equation. Changing any one of them will alter the parabola in a predictable way. Understanding these relationships is key to mastering quadratic equations. Think of each coefficient as a dial that you can adjust to fine-tune the shape and position of the curve.

Solving for 'x'
3. Methods for Unearthing the Solutions
Okay, so we know what ax2 + bx + c is and what the coefficients do. But how do we actually solve for 'x'? That is, how do we find the values of 'x' that make the equation equal to zero? There are a few common methods, each with its own strengths and weaknesses.
First up, we have factoring. This method involves breaking down the quadratic expression into two binomials (expressions with two terms). If you can factor the expression, you can then set each binomial equal to zero and solve for 'x'. This is often the quickest method, but it only works for certain quadratic equations—those that can be neatly factored. It's like finding the perfect puzzle pieces that fit together effortlessly. When factoring doesn't work, you'll need to bring out the big guns.
Next, we have the quadratic formula. This is the heavy artillery of quadratic equations. It works for any quadratic equation, regardless of whether it can be factored. The formula itself looks a bit intimidating: x = (-b (b2 - 4ac)) / 2a. But don't let that scare you! Once you get the hang of plugging in the values of a, b, and c, it becomes a reliable method for finding the solutions.
Finally, we have completing the square. This method involves manipulating the quadratic equation to create a perfect square trinomial (a trinomial that can be factored into the square of a binomial). It's a bit more involved than factoring or using the quadratic formula, but it's a powerful technique that can be useful in other areas of algebra. It's like taking something incomplete and transforming it into something whole and perfect.
Real-World Applications
4. From Physics to Finance
So, we've gone through the theory. But where does all this actually matter? As it turns out, quadratic equations are incredibly useful in a wide variety of real-world applications. Let's take a look at a few examples.
In physics, quadratic equations are used to model projectile motion. When you throw a ball, its trajectory follows a parabolic path, which can be described using a quadratic equation. Engineers use this knowledge to design everything from catapults to rockets. It's like having the power to predict the future path of objects in motion!
In finance, quadratic equations can be used to model profit and loss. For example, a business might use a quadratic equation to determine the optimal price point for a product to maximize its profit. They can also be used to calculate compound interest and other financial calculations. It's like having a mathematical crystal ball to see into the financial future!
Even in computer graphics and game development, quadratic equations play a crucial role. They're used to create curves and surfaces, to simulate physics, and to design realistic-looking environments. Next time you're playing a video game, remember that quadratic equations are working behind the scenes to bring the game to life.

Beyond the Basics
5. Venturing Further into the Quadratic Realm
Now that you've got a solid grasp of the basics, let's briefly touch upon some more advanced concepts related to quadratic equations. This is where things start to get really interesting!
One important concept is the discriminant, which is the expression b2 - 4ac that appears under the square root in the quadratic formula. The discriminant tells us about the nature of the solutions to the quadratic equation. If the discriminant is positive, there are two distinct real solutions. If the discriminant is zero, there is one real solution (a repeated root). And if the discriminant is negative, there are no real solutions (only complex solutions). It's like a mathematical fortune teller, revealing the secrets of the solutions before you even solve the equation!
Another advanced concept is the relationship between the roots (solutions) of a quadratic equation and its coefficients. If the roots are r1 and r2, then the quadratic equation can be written as a(x - r1)(x - r2) = 0. This means that the sum of the roots is -b/a and the product of the roots is c/a. Knowing these relationships can be helpful in solving problems where you're given information about the roots rather than the coefficients.
Finally, there are higher-degree polynomial equations that build upon the principles of quadratic equations. While these equations are more complex, they often involve techniques and concepts that are similar to those used for quadratic equations. So, mastering quadratic equations is a crucial stepping stone to understanding more advanced algebraic concepts.
